| The law of atmospheres, also known as the barometric law, states that the pressure n(y) as a function of height y varies as: | |
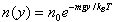 | |
According to the ideal gas law, a gas of N particles in the thermal equilibrium obeys the relationship PV = NkBT. It is convenient to rewrite this equation in terms of the number of particles per unit volume of gas, nV = N/V. This quantity is important because it can vary from one point to another. In fact, our goal is to determine how nVchanges in our atmosphere. We can express the ideal gas law in terms of nV as P = nVkBT. Thus, if the number density nV is known, we can find the pressure and vice versa. | |
| The pressure in the atmosphere decreases as the altitude increases because a given layer of air has to support the weight of the air above it — the greater the altitude, the less the weight of the air above that layer and the lower the pressure. | |
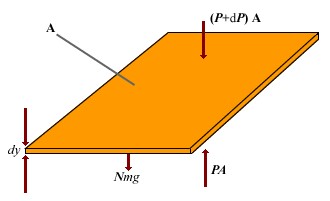 | |
To determine the variation in pressure with altitude, consider an atmospheric layer of thickness dy and the cross-sectional area A. Because the air is in static equilibrium, the upward force on the bottom of this layer, PA, must exceed the downward force on the top of the layer, (P + dP)A, by an amount equal to the weight of gas in this thin layer. If the mass of gas molecule in the layer is m, and the area a total of N molecules in the layer, then the weight of the layer is w = mgN = mgnVAdy. Thus A - (P + dP)A = mgnVAdy, Which reduces to dP = - mgnVdyBecause P = nVkBT, and T is assumed to remain constant, therefore dP = nVkBT dnV. | |
| Substituting this into the above expression for dP and rearranging gives | |
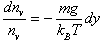 | |
| Integrating this expression, we find | |
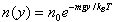 | |
| Boltzmann distribution law | |
Boltzmann distribution law is important in describing the statistical mechanics of a large number of particles. It states that the probability of finding the particles in a particular energy state varies exponentially as the negative of the energy divided by kBT. All the particles would fall into the lowest energy level, except that the thermal energy kBT tends to excite the particles to higher energy levels. | |
Distribution of particles in space is | |
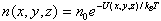 | |
| Where n0 is the number of particles where U = 0 This king of distribution applies to any energy the particles have, such as kinetic energy. In general, the relative number of particles having energy E is | |
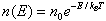 | |
Style2
Style3[OneLeft]
Style3[OneRight]
Style4
Style5
Tagged with: Engineering/Science Laws
About engineer eye
This is a short description in the author block about the author. You edit it by entering text in the "Biographical Info" field in the user admin panel.
Subscribe to:
Post Comments (Atom)
- Popular Post
- Video
- Category
Pel�culas populares
-
A compound wound dc motor or rather a dc compound motor falls under the category of self excited motors, and is made up of both series ...
-
Welcome to this open and free electrical engineering study site. A strong team of well experienced electrical engineers in different fields...
-
RC PLANE DESIGN Wing design Explanation We used Dihedral wing, which helps to increase the gliding time with less battery charge. ...
-
Use these tips and instructions for adding new electrical wiring. Take a few minutes to read the directions thoroughly. Foll...
-
Definition of the ampere : If two long, parallel wires 1 m apart carry the same current and the force per unit length on each wire is 2x10 ...
-
These force laws, together with the laws of motion, are the foundations of classical mechanics. They are based on experimental observations...
-
Shortly after Oersted's discovery in 1819 that a compass needle is deflected by a current-carrying conductor, Jean Baptist Biot and F...
-
Insulation Resistance of Cable Joules Laws of Heating Laws of Resistance What is conductivity? Working Principle of DC Motor Working Pr...
-
Ohm's law was named after George Simon Ohm (1787 — 1854). It states that for many materials (including most metals), the ratio of the...
No comments: