Ampere's Law

Definition of the ampere: If two long, parallel wires 1 m apart carry the same current and the force per unit length on each wire is 2x10-7N/m, then the current is defined to be 1 A. Consider two long, straight, parallel wires separated by a distance a and carrying currents  I1 and I2 in the same direction. We can easily determine the force on one wire due to a magnetic field set up by the other wire.  Wire 2, which carries a current I2, creates a magnetic field B2 at the position of wire 1. The direction of B2 is perpendicular to wire1.

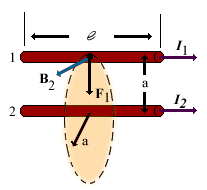The magnitude force on a length l of wire 1 is

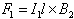Sincel is perpendicular to B2, the magnitude of F1 is

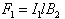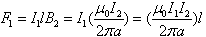We can rewrite this in terms of the force per unit length as

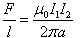The numerical value of 2x10-7 N/m is obtained from the equation above with I1= I2= 1 A and a = 1 m. The Ampère's law states that the line integral of B.ds around any closed path equals 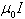, where  I is the total steady current passing through any surface bounded by closed path

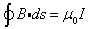Ampère's law is valid only for steady currents and is useful only for calculating the magnetic field of current configurations having a high degree of symmetry.