Electrical Engineering Video
Posted by: engineer eye Posted date: 6:40 AM / comment : 0 Electrical, Engineering/Science Laws
Faraday's Law of Induction
In physics, a quantitative relationship between a changing magnetic field and the electric field created by the change, developed on the basis of experimental observations made in 1831 by the English scientist Michael Faraday.
Faraday discovered that, whenever the magnetic field about an electromagnet was made to grow and collapse by closing and opening the electric circuit of which it was a part, an electric current could be detected in a separate conductor nearby. Moving a permanent magnet into and out of a coil of wire also induced a current in the wire while the magnet was in motion. Moving a conductor near a stationary permanent magnet caused a current to flow in the wire, too, as long as it was moving.
Faraday visualized a magnetic field as composed of many lines of induction, along which a small magnetic compass would point. The aggregate of the lines intersecting a given area is called the magnetic flux. The electrical effects were thus attributed by Faraday to a changing magnetic flux.
Years later the Scottish physicist James Clerk Maxwell proposed that the fundamental effect of changing magnetic flux was the production of an electric field, not only in a conductor but also in space even in the absence of electric charges. Maxwell formulated the mathematical expression relating the change in magnetic flux to the induced electromotive force (E, or emf).
This relationship, known as Faraday's law of induction, states that the magnitude of the emf induced in a circuit is proportional to the rate of change of the magnetic flux that cuts across the circuit.
If the rate of change of magnetic flux is expressed in units of webers per second, the induced emf has units of volts.
Faraday discovered that, whenever the magnetic field about an electromagnet was made to grow and collapse by closing and opening the electric circuit of which it was a part, an electric current could be detected in a separate conductor nearby. Moving a permanent magnet into and out of a coil of wire also induced a current in the wire while the magnet was in motion. Moving a conductor near a stationary permanent magnet caused a current to flow in the wire, too, as long as it was moving.
Faraday visualized a magnetic field as composed of many lines of induction, along which a small magnetic compass would point. The aggregate of the lines intersecting a given area is called the magnetic flux. The electrical effects were thus attributed by Faraday to a changing magnetic flux.
Years later the Scottish physicist James Clerk Maxwell proposed that the fundamental effect of changing magnetic flux was the production of an electric field, not only in a conductor but also in space even in the absence of electric charges. Maxwell formulated the mathematical expression relating the change in magnetic flux to the induced electromotive force (E, or emf).
This relationship, known as Faraday's law of induction, states that the magnitude of the emf induced in a circuit is proportional to the rate of change of the magnetic flux that cuts across the circuit.
If the rate of change of magnetic flux is expressed in units of webers per second, the induced emf has units of volts.
Ampere's Law
| Definition of the ampere: If two long, parallel wires 1 m apart carry the same current and the force per unit length on each wire is 2x10-7N/m, then the current is defined to be 1 A. Consider two long, straight, parallel wires separated by a distance a and carrying currents I1 and I2 in the same direction. We can easily determine the force on one wire due to a magnetic field set up by the other wire. Wire 2, which carries a current I2, creates a magnetic field B2 at the position of wire 1. The direction of B2 is perpendicular to wire1. | |
 | |
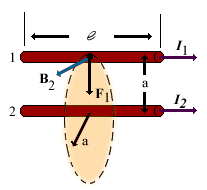The magnitude force on a length l of wire 1 is | |
 | |
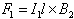Sincel is perpendicular to B2, the magnitude of F1 is | |
 | |
 | |
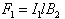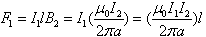We can rewrite this in terms of the force per unit length as | |
 | |
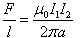| The numerical value of 2x10-7 N/m is obtained from the equation above with I1= I2= 1 A and a = 1 m. The Ampère's law states that the line integral of B.ds around any closed path equals 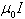 , where I is the total steady current passing through any surface bounded by closed path | |
 | |
| Ampère's law is valid only for steady currents and is useful only for calculating the magnetic field of current configurations having a high degree of symmetry. | |
Kepler's Laws
The German astronomer Johannes Kepler, who was Brahe's assistant, acquired Brahe's astronomical data and spent about 16 years trying to deduce a mathematical model for the motion of the planets. After many laborious calculations, he found that Brahe's precise data on the resolution of Mars about the Sun provided the answer. Such data are difficult to sort out because the Earth is also in motion about the Sun.
 |
| Kepler's analysis first showed that the concept of circular orbits about the Sun had to be abandoned. He eventually discovered that the orbit of Mars could be accurately described by an ellipse with the Sun at one focal point. He then generalized this analysis to include the motion of all planets. The complete analysis is summarized in three statements, known as Kepler's laws: |
| 1. | All planets move in elliptical orbits with the Sun at one of the focal points. |
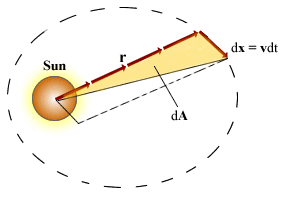
| 2. | The radius vector drawn from the Sun to a planet sweeps out equal areas in equal time intervals. |
| 3. | The square of the orbital period of any planet is proportional to the cube of the semimajor axis of the elliptical orbit. |
Half century later, Newton demonstrated that these laws are the consequence of a simple force that exists between any two masses. Newton's law of gravity, together with his development of the laws of motion, provides the basis for a full mathematical solution to the motion of planets and satellites. More important, Newton's law of gravity correctly describes the gravitational attractive force between any two masses. |
| Mathematical statements: | |
| Kepler's second law | |
 | |
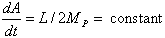| Where dA is the area swept by radius vector r in a time dt and Mp is the planet mass. | |
| Kepler's third law | |
 | |
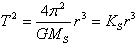| Where KS is a constant given by | |
 | |
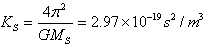| MS is the Sun mass, G is universal gravitational constant and T is the time. | |
Law of Atmospheres and Boltzmann Law
| The law of atmospheres, also known as the barometric law, states that the pressure n(y) as a function of height y varies as: | |
 | |
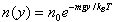According to the ideal gas law, a gas of N particles in the thermal equilibrium obeys the relationship PV = NkBT. It is convenient to rewrite this equation in terms of the number of particles per unit volume of gas, nV = N/V. This quantity is important because it can vary from one point to another. In fact, our goal is to determine how nVchanges in our atmosphere. We can express the ideal gas law in terms of nV as P = nVkBT. Thus, if the number density nV is known, we can find the pressure and vice versa. | |
| The pressure in the atmosphere decreases as the altitude increases because a given layer of air has to support the weight of the air above it — the greater the altitude, the less the weight of the air above that layer and the lower the pressure. | |
 | |
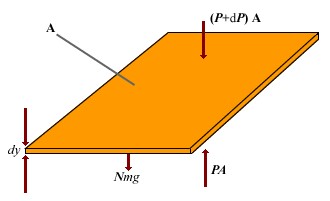To determine the variation in pressure with altitude, consider an atmospheric layer of thickness dy and the cross-sectional area A. Because the air is in static equilibrium, the upward force on the bottom of this layer, PA, must exceed the downward force on the top of the layer, (P + dP)A, by an amount equal to the weight of gas in this thin layer. If the mass of gas molecule in the layer is m, and the area a total of N molecules in the layer, then the weight of the layer is w = mgN = mgnVAdy. Thus A - (P + dP)A = mgnVAdy, Which reduces to dP = - mgnVdyBecause P = nVkBT, and T is assumed to remain constant, therefore dP = nVkBT dnV. | |
| Substituting this into the above expression for dP and rearranging gives | |
 | |
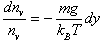| Integrating this expression, we find | |
| |
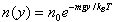| Boltzmann distribution law | |
Boltzmann distribution law is important in describing the statistical mechanics of a large number of particles. It states that the probability of finding the particles in a particular energy state varies exponentially as the negative of the energy divided by kBT. All the particles would fall into the lowest energy level, except that the thermal energy kBT tends to excite the particles to higher energy levels. | |
Distribution of particles in space is | |
 | |
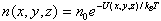| Where n0 is the number of particles where U = 0 This king of distribution applies to any energy the particles have, such as kinetic energy. In general, the relative number of particles having energy E is | |
 | |
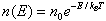Subscribe to:
Posts (Atom)
Pel�culas populares
-
Shortly after Oersted's discovery in 1819 that a compass needle is deflected by a current-carrying conductor, Jean Baptist Biot and F...
-
A compound wound dc motor or rather a dc compound motor falls under the category of self excited motors, and is made up of both series ...
-
There are a few forms of this rule, and it can be applied in many ways. Originally, it was a trick for right-handed coordinate systems to ...
-
These force laws, together with the laws of motion, are the foundations of classical mechanics. They are based on experimental observations...
-
RC PLANE DESIGN Wing design Explanation We used Dihedral wing, which helps to increase the gliding time with less battery charge. ...
-
Use these tips and instructions for adding new electrical wiring. Take a few minutes to read the directions thoroughly. Foll...
-
Welcome to this open and free electrical engineering study site. A strong team of well experienced electrical engineers in different fields...
-
Image: Ocean Power Technologies Aerospace giant Lockheed Martin recently signed a contract to build the world’s largest wave energy farm,...
-
In physics, a quantitative relationship between a changing magnetic field and the electric field created by the change, developed on the b...
-
Definition of the ampere : If two long, parallel wires 1 m apart carry the same current and the force per unit length on each wire is 2x10 ...
